地球上の緯度1度、経度1度は実際どれくらいの長さがあるのでしょうか。これが今回のテーマです。同じネタは他のブログや Yahoo知恵袋などで扱われているのですが、どれも地球を球として計算しているので、ここでは地球を回転楕円体として計算し、1度ずつ厳密に求めてみます。
経度1度間の距離
私は(現在のところ)年に数回GISソフトウェアの実習講座を行っているのですが、GISは空間参照を理解しなければ正しい使い方ができません。そのため測地系や投影法の説明をする単元を用意しており、その中で毎回こんな質問します。
下の図を見てください。
緯度0度、つまり赤道上で東経135度から東経136度までの経線間の距離は約111kmです。日本の関西地方付近である北緯35度上で東経135度から東経136度までの経線間の距離は約91kmです。
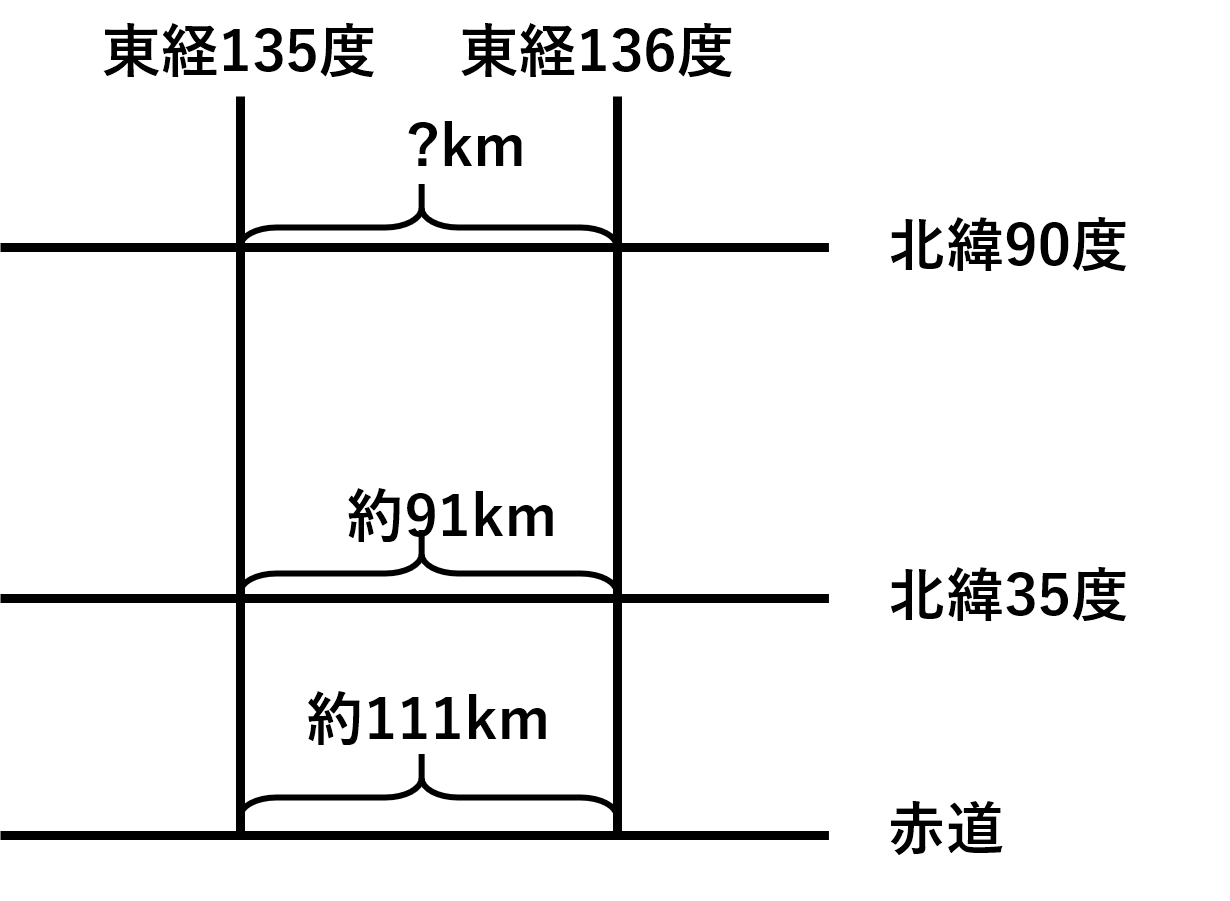

では北緯90度上で経度135度から経度136度までの経線間の距離は何キロメートルでしょうか?
…
大人になると自分から手を挙げて回答するのは恥ずかしいですよね?では4択で手を挙げてください。
1.赤道上の距離と同じだと思う人?
2.赤道上の距離より短いと思う人?
3.赤道上の距離より長いと思う人?
というと、半分くらいが「2.」を選びますが、他の半分はまごまごします。ここで、
北緯90度ってどこですかね?
というと、半分くらいが
あっ(察し)
という顔になり、
北緯90度は北極点です。つまり北極点から北極点までの距離なので 0km です。
と答えるとほとんどの人が
なんだそんな簡単な問題か。
という顔をします。
この問題は私の受け持つ講座で延べ300人ぐらいには質問してきましたが、正解が答えられた人はこれまで 4人しかいません。その4人は一瞬で「0です。」と答えてくれたのですが、ほとんどの方が地図を専門に仕事をしている訳ではないためか答えられません。中学校の社会科で習ったはずなのに。世の中には地球平面協会という地球が平らだと本気で主張している人たちがいますが、彼らを笑うことはできないのです。
多くの人が答えられない原因は、緯度と経度が平面上で直交しているイメージしか持てないからだと考えます。メルカトル図法がその良い例です。私の質問ではホワイトボードにあえて緯度と経度を直交して書くのですが、このように書かれると地球が丸いことを忘れてしまうようです。
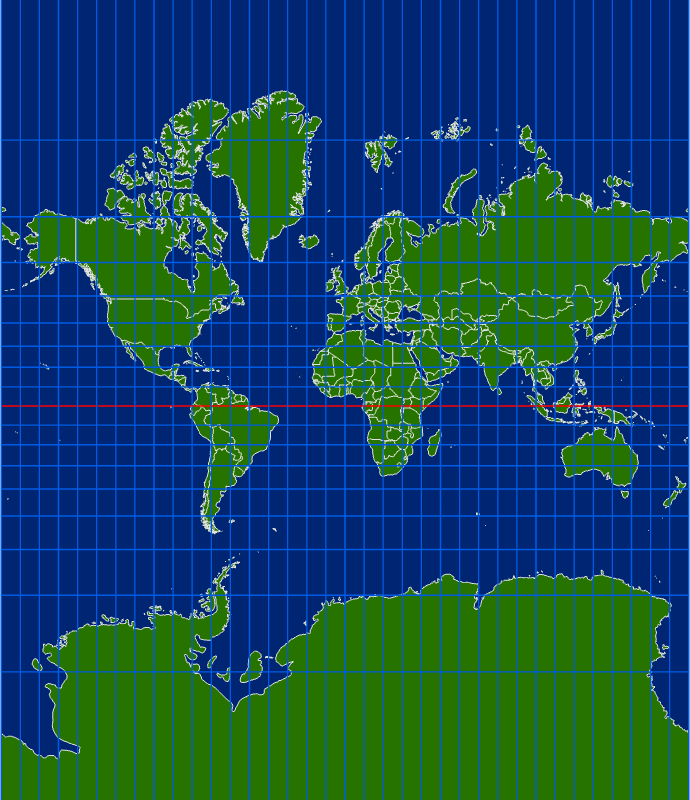

メルカトル図法
地球は丸いんだよ。僕を見て思い出して。
Google Maps の投影法が変更
そんな認識の問題もあってか、2018年8月3日に Google Mapsはデフォルト設定が宇宙から見たように表現される外射図法に変更されました(従来のメルカトル図法で表示することもできます)。こちらの記事では正射図法と結論づけられています。
正射図法で世界を示すと「北緯90度上で経度135度から経度136度までの経線間の距離」は 0m であることがよく分かります。
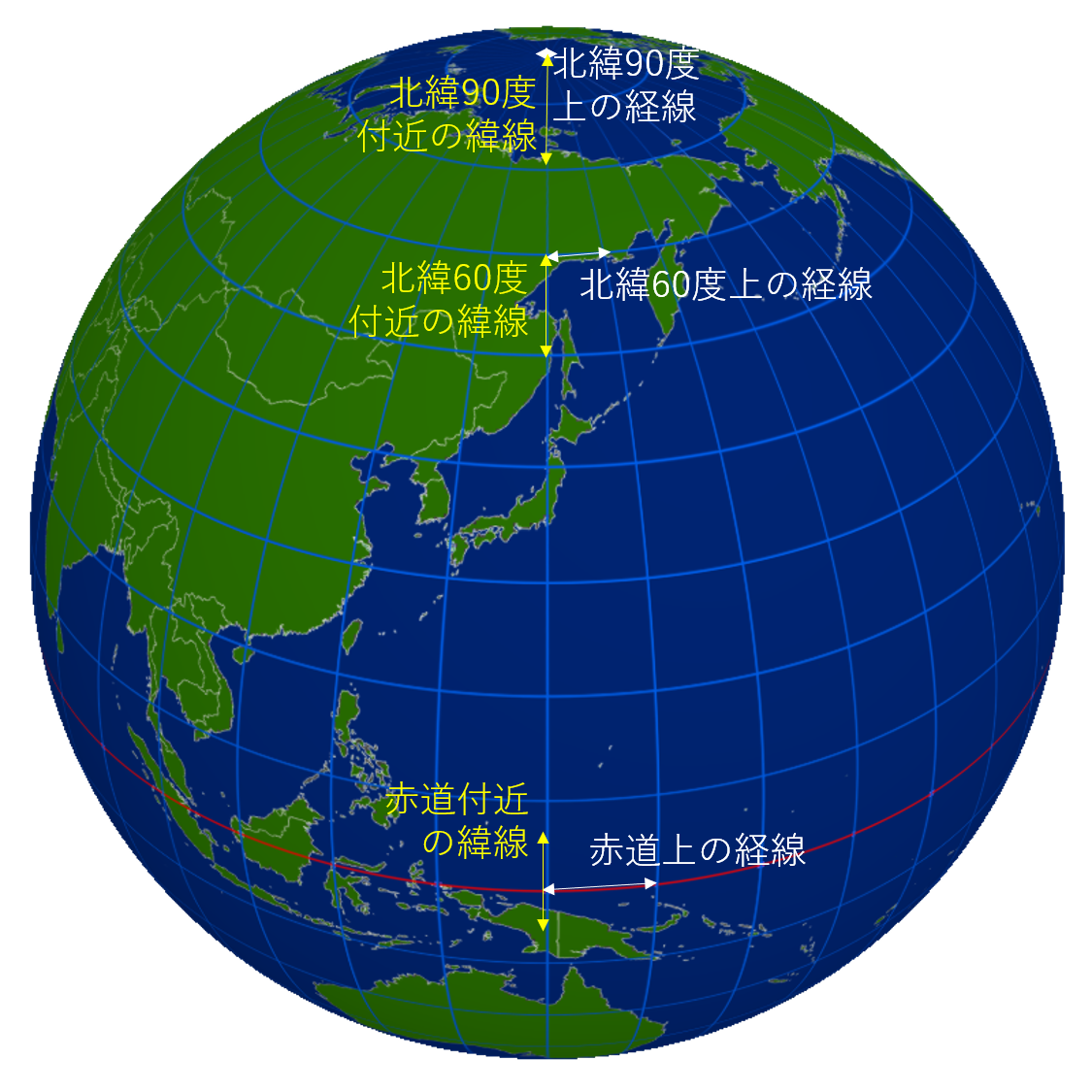

外射図法
地球は丸いことを改めて認識したところで、冒頭の緯度・経度の 1度はどれくらいの距離があるのか考えてみます。
前提条件
地球の大きさには様々な定義がありますが、今回は赤道半径と極半径が異なる WGS84 楕円体を使用します。
WGS84楕円体
赤道半径:6,378,137m、偏平率の逆数:298.257223563
GCS_WGS_1984 (4326)
回転楕円体における計算式で長さを求めることもできますが、難しい計算はArcGISにやらせようということでarcpyというAPIを使用して計算しました。
経度0度上で北緯0度~90度まで1度ずつの間隔で点を置き、その点から経度を+1度とした2点、緯度は+-0.5度して求めた2点で「東西・南北における 1度の線分」を作成します。作成した線分の測地線距離を測定します。
緯度・経度で1度、1分の距離と、その場所の測地線距離1mが何度相当になるかを求めました。測地線距離の説明はこちらの記事をご覧ください。


緯度・経度1度の距離と1mの角距離
| 緯度 | 経度1度長 (m) | 緯度1度長 (m) | 経度1分長 (m) | 緯度1分長 (m) | 経度1m角 (度) | 緯度1m角 (度) |
|---|---|---|---|---|---|---|
| 90 | 0 | ? | 0 | ? | None | ? |
| 89 | 1949.302 | 111693.607 | 32.4884 | 1861.5601 | 0.0005130041 | 0.0000089531 |
| 88 | 3897.9983 | 111692.5757 | 64.9666 | 1861.5429 | 0.0002565419 | 0.0000089531 |
| 87 | 5845.4833 | 111690.8584 | 97.4247 | 1861.5143 | 0.0001710723 | 0.0000089533 |
| 86 | 7791.152 | 111688.457 | 129.8525 | 1861.4743 | 0.0001283507 | 0.0000089535 |
| 85 | 9734.4 | 111685.3748 | 162.24 | 1861.4229 | 0.0001027285 | 0.0000089537 |
| 84 | 11674.6236 | 111681.6154 | 194.5771 | 1861.3603 | 0.0000856559 | 0.0000089540 |
| 83 | 13611.2206 | 111677.1837 | 226.8537 | 1861.2864 | 0.0000734688 | 0.0000089544 |
| 82 | 15543.5895 | 111672.0851 | 259.0598 | 1861.2014 | 0.0000643352 | 0.0000089548 |
| 81 | 17471.1309 | 111666.326 | 291.1855 | 1861.1054 | 0.0000572373 | 0.0000089553 |
| 80 | 19393.2468 | 111659.9135 | 323.2208 | 1860.9986 | 0.0000515643 | 0.0000089558 |
| 79 | 21309.3412 | 111652.8558 | 355.1557 | 1860.8809 | 0.0000469278 | 0.0000089563 |
| 78 | 23218.8202 | 111645.1615 | 386.9803 | 1860.7527 | 0.0000430685 | 0.0000089569 |
| 77 | 25121.0924 | 111636.8403 | 418.6849 | 1860.614 | 0.0000398072 | 0.0000089576 |
| 76 | 27015.5689 | 111627.9025 | 450.2595 | 1860.465 | 0.0000370157 | 0.0000089583 |
| 75 | 28901.6635 | 111618.3593 | 481.6944 | 1860.306 | 0.0000346001 | 0.0000089591 |
| 74 | 30778.7931 | 111608.2226 | 512.9799 | 1860.137 | 0.0000324899 | 0.0000089599 |
| 73 | 32646.3777 | 111597.505 | 544.1063 | 1859.9584 | 0.0000306313 | 0.0000089608 |
| 72 | 34503.8407 | 111586.2197 | 575.064 | 1859.7703 | 0.0000289823 | 0.0000089617 |
| 71 | 36350.6089 | 111574.3809 | 605.8435 | 1859.573 | 0.0000275099 | 0.0000089626 |
| 70 | 38186.1133 | 111562.0033 | 636.4352 | 1859.3667 | 0.0000261875 | 0.0000089636 |
| 69 | 40009.7884 | 111549.1022 | 666.8298 | 1859.1517 | 0.0000249939 | 0.0000089647 |
| 68 | 41821.0731 | 111535.6936 | 697.0179 | 1858.9282 | 0.0000239114 | 0.0000089657 |
| 67 | 43619.4106 | 111521.7943 | 726.9902 | 1858.6966 | 0.0000229256 | 0.0000089669 |
| 66 | 45404.2485 | 111507.4213 | 756.7375 | 1858.457 | 0.0000220244 | 0.0000089680 |
| 65 | 47175.0392 | 111492.5926 | 786.2507 | 1858.2099 | 0.0000211977 | 0.0000089692 |
| 64 | 48931.2401 | 111477.3265 | 815.5207 | 1857.9554 | 0.0000204368 | 0.0000089704 |
| 63 | 50672.3134 | 111461.6419 | 844.5386 | 1857.694 | 0.0000197346 | 0.0000089717 |
| 62 | 52397.7267 | 111445.5582 | 873.2954 | 1857.426 | 0.0000190848 | 0.0000089730 |
| 61 | 54106.9529 | 111429.0952 | 901.7825 | 1857.1516 | 0.0000184819 | 0.0000089743 |
| 60 | 55799.4704 | 111412.2734 | 929.9912 | 1856.8712 | 0.0000179213 | 0.0000089757 |
| 59 | 57474.7635 | 111395.1134 | 957.9127 | 1856.5852 | 0.0000173989 | 0.0000089771 |
| 58 | 59132.3223 | 111377.6364 | 985.5387 | 1856.2939 | 0.0000169112 | 0.0000089785 |
| 57 | 60771.6427 | 111359.864 | 1012.8607 | 1855.9977 | 0.0000164550 | 0.0000089799 |
| 56 | 62392.2272 | 111341.818 | 1039.8705 | 1855.697 | 0.0000160276 | 0.0000089814 |
| 55 | 63993.5843 | 111323.5206 | 1066.5597 | 1855.392 | 0.0000156266 | 0.0000089828 |
| 54 | 65575.229 | 111304.9944 | 1092.9205 | 1855.0832 | 0.0000152497 | 0.0000089843 |
| 53 | 67136.683 | 111286.2621 | 1118.9447 | 1854.771 | 0.0000148950 | 0.0000089858 |
| 52 | 68677.4748 | 111267.3466 | 1144.6246 | 1854.4558 | 0.0000145608 | 0.0000089874 |
| 51 | 70197.1396 | 111248.2712 | 1169.9523 | 1854.1379 | 0.0000142456 | 0.0000089889 |
| 50 | 71695.2196 | 111229.0593 | 1194.9203 | 1853.8177 | 0.0000139479 | 0.0000089905 |
| 49 | 73171.2644 | 111209.7343 | 1219.5211 | 1853.4956 | 0.0000136666 | 0.0000089920 |
| 48 | 74624.8305 | 111190.3199 | 1243.7472 | 1853.172 | 0.0000134004 | 0.0000089936 |
| 47 | 76055.482 | 111170.8398 | 1267.5914 | 1852.8473 | 0.0000131483 | 0.0000089952 |
| 46 | 77462.7903 | 111151.3178 | 1291.0465 | 1852.522 | 0.0000129094 | 0.0000089967 |
| 45 | 78846.3347 | 111131.7777 | 1314.1056 | 1852.1963 | 0.0000126829 | 0.0000089983 |
| 44 | 80205.7019 | 111112.2433 | 1336.7617 | 1851.8707 | 0.0000124679 | 0.0000089999 |
| 43 | 81540.4864 | 111092.7384 | 1359.0081 | 1851.5456 | 0.0000122638 | 0.0000090015 |
| 42 | 82850.2908 | 111073.2868 | 1380.8382 | 1851.2214 | 0.0000120700 | 0.0000090031 |
| 41 | 84134.7255 | 111053.9121 | 1402.2454 | 1850.8985 | 0.0000118857 | 0.0000090046 |
| 40 | 85393.4091 | 111034.6377 | 1423.2235 | 1850.5773 | 0.0000117105 | 0.0000090062 |
| 39 | 86625.9685 | 111015.4872 | 1443.7661 | 1850.2581 | 0.0000115439 | 0.0000090078 |
| 38 | 87832.0385 | 110996.4837 | 1463.8673 | 1849.9414 | 0.0000113854 | 0.0000090093 |
| 37 | 89011.2625 | 110977.6503 | 1483.521 | 1849.6275 | 0.0000112345 | 0.0000090108 |
| 36 | 90163.2924 | 110959.0097 | 1502.7215 | 1849.3168 | 0.0000110910 | 0.0000090123 |
| 35 | 91287.7885 | 110940.5844 | 1521.4631 | 1849.0097 | 0.0000109544 | 0.0000090138 |
| 34 | 92384.4194 | 110922.3968 | 1539.7403 | 1848.7066 | 0.0000108243 | 0.0000090153 |
| 33 | 93452.8629 | 110904.4688 | 1557.5477 | 1848.4078 | 0.0000107006 | 0.0000090168 |
| 32 | 94492.805 | 110886.822 | 1574.8801 | 1848.1137 | 0.0000105828 | 0.0000090182 |
| 31 | 95503.9408 | 110869.4777 | 1591.7323 | 1847.8246 | 0.0000104708 | 0.0000090196 |
| 30 | 96485.9741 | 110852.4568 | 1608.0996 | 1847.5409 | 0.0000103642 | 0.0000090210 |
| 29 | 97438.6175 | 110835.7798 | 1623.977 | 1847.263 | 0.0000102629 | 0.0000090224 |
| 28 | 98361.5928 | 110819.4667 | 1639.3599 | 1846.9911 | 0.0000101666 | 0.0000090237 |
| 27 | 99254.6306 | 110803.5371 | 1654.2438 | 1846.7256 | 0.0000100751 | 0.0000090250 |
| 26 | 100117.4705 | 110788.0101 | 1668.6245 | 1846.4668 | 0.0000099883 | 0.0000090262 |
| 25 | 100949.8614 | 110772.9044 | 1682.4977 | 1846.2151 | 0.0000099059 | 0.0000090275 |
| 24 | 101751.5613 | 110758.2381 | 1695.8594 | 1845.9706 | 0.0000098279 | 0.0000090287 |
| 23 | 102522.3372 | 110744.0288 | 1708.7056 | 1845.7338 | 0.0000097540 | 0.0000090298 |
| 22 | 103261.9655 | 110730.2935 | 1721.0328 | 1845.5049 | 0.0000096841 | 0.0000090310 |
| 21 | 103970.2317 | 110717.0485 | 1732.8372 | 1845.2841 | 0.0000096181 | 0.0000090320 |
| 20 | 104646.9309 | 110704.3098 | 1744.1155 | 1845.0718 | 0.0000095559 | 0.0000090331 |
| 19 | 105291.8673 | 110692.0926 | 1754.8645 | 1844.8682 | 0.0000094974 | 0.0000090341 |
| 18 | 105904.8544 | 110680.4115 | 1765.0809 | 1844.6735 | 0.0000094424 | 0.0000090350 |
| 17 | 106485.7152 | 110669.2804 | 1774.7619 | 1844.488 | 0.0000093909 | 0.0000090359 |
| 16 | 107034.2822 | 110658.7126 | 1783.9047 | 1844.3119 | 0.0000093428 | 0.0000090368 |
| 15 | 107550.3973 | 110648.7207 | 1792.5066 | 1844.1453 | 0.0000092980 | 0.0000090376 |
| 14 | 108033.9117 | 110639.3166 | 1800.5652 | 1843.9886 | 0.0000092564 | 0.0000090384 |
| 13 | 108484.6862 | 110630.5115 | 1808.0781 | 1843.8419 | 0.0000092179 | 0.0000090391 |
| 12 | 108902.5913 | 110622.3159 | 1815.0432 | 1843.7053 | 0.0000091825 | 0.0000090398 |
| 11 | 109287.5068 | 110614.7396 | 1821.4584 | 1843.579 | 0.0000091502 | 0.0000090404 |
| 10 | 109639.3221 | 110607.7916 | 1827.322 | 1843.4632 | 0.0000091208 | 0.0000090410 |
| 9 | 109957.9362 | 110601.4802 | 1832.6323 | 1843.358 | 0.0000090944 | 0.0000090415 |
| 8 | 110243.2576 | 110595.8128 | 1837.3876 | 1843.2635 | 0.0000090708 | 0.0000090419 |
| 7 | 110495.2045 | 110590.7962 | 1841.5867 | 1843.1799 | 0.0000090502 | 0.0000090423 |
| 6 | 110713.7047 | 110586.4363 | 1845.2284 | 1843.1073 | 0.0000090323 | 0.0000090427 |
| 5 | 110898.6955 | 110582.7384 | 1848.3116 | 1843.0456 | 0.0000090172 | 0.0000090430 |
| 4 | 111050.124 | 110579.7068 | 1850.8354 | 1842.9951 | 0.0000090049 | 0.0000090433 |
| 3 | 111167.9466 | 110577.3452 | 1852.7991 | 1842.9558 | 0.0000089954 | 0.0000090434 |
| 2 | 111252.1298 | 110575.6563 | 1854.2022 | 1842.9276 | 0.0000089886 | 0.0000090436 |
| 1 | 111302.6493 | 110574.6422 | 1855.0442 | 1842.9107 | 0.0000089845 | 0.0000090437 |
| 0 | 111319.4908 | 110574.304 | 1855.3248 | 1842.9051 | 0.0000089832 | 0.0000090437 |
北緯 90度における緯度1度の距離は求めることができますが作成したコードだと0で除算することになるので89度までの処理としました。
この結果を見ると、以前に書いた1マイルの距離を求めた記事でも触れたように、厳密には緯度の場所によって緯度1度の距離も異なることが分かります。緯度1度の長さは極付近で最大となり、赤道へ近づくにつれて微妙に短くなります。経度は赤道が最長で極が0となります。緯度1度と経度1度の距離がほぼ等しいのは緯度5度~6度の間ということが分かります。また、以前に書いた地理座標系のデータをそのまま距離に関連する空間解析を行う際に指定するべき Z係数の値ですが、Esriのブログで提示された係数は「"経度"間1m相当の角距離」であることが分かりました。より厳密に係数を求めたい場合はこちらの表が利用できます。


ソースコード
Pythonウィンドウにそのまま貼り付けてご利用ください。ArcMap 10.4、AcGIS Pro 1.3、ArcGIS Pro 2.2で動作確認しております。arcpy.SpatialReferenceの引数であるEPSG番号を変更して一般的に使用される球体としての地球で計算することもできます。
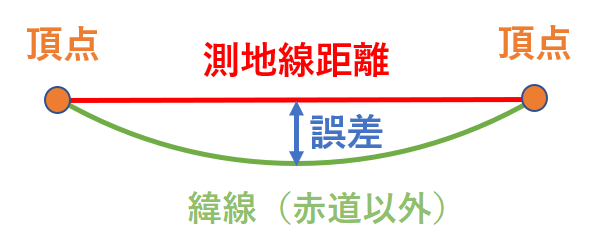
なお、arcpyを含め、ArcGISで計測される線分の距離は頂点間となります。同一緯線上では赤道以外、線分の両端の最短距離(測地線距離を求めるための線分)と、緯線の長さは微妙に一致しませんが、経度1度間では約100kmに対して1m程度と微々たる誤差だったので無視しました。経度の距離間が長くなると誤差は大きくなるので、より正確に求めたいならば、arcpy.Polylineで生成したポリラインをdensifyで細かく頂点分割してください。

#coding:UTF-8
# ArcGIS での距離計測
# 地球上の1度間の測地線距離を計算
# 経度0度、北緯0度~90度を中心とした東西1度、南北1度の測地線距離を計算
# ArcGIS Pro 2.2, ArcGIS Pro 1.3, ArcMap 10.4.1で動作確認
import arcpy
# WGS84楕円体
# 赤道半径:6,378,137m、扁平率の逆数:298.257223563
# GCS_WGS_1984 (4326)
gcs = arcpy.SpatialReference(4326)
# 天文学における地球半径
# 赤道半径:6,371,000m、扁平率の逆数:0
# Authalic Shpere GCS_Shpere GCS_Sphere (4035)
#gcs = arcpy.SpatialReference(4035)
print("Spatial Reference: {0} ({1})".format(gcs.GCSName, gcs.GCSCode))
print("{}\t{}\t{}\t{}\t{}\t{}\t{}".format("緯度", "経度1度長 (m)".ljust(10), "緯度1度長 (m)".ljust(10), "経度1分長 (m)".ljust(10),
"緯度1分長 (m)".ljust(10), "経度1m角 (度)".ljust(10), "緯度1m角 (度)".ljust(10)))
print("{}\t{}\t{}\t{}\t{}\t{}\t{}".format("90", "0".ljust(10), "?".ljust(10), "0".ljust(10),
"?".ljust(10), "None".ljust(10), "?".ljust(10)))
for lat in range(89, -1, -1):
# 経度
point_width_from = arcpy.Point(0, lat)
point_width_to = arcpy.Point(1, lat)
polyline_width = arcpy.Polyline(arcpy.Array([point_width_from, point_width_to]), gcs)
length_width = polyline_width.getLength("GEODESIC")
# 緯度
point_height_from = arcpy.Point(0, lat - 0.5)
point_height_to = arcpy.Point(0, lat + 0.5)
polyline_height = arcpy.Polyline(arcpy.Array([point_height_from, point_height_to]), gcs)
length_height = polyline_height.getLength("GEODESIC")
print("{:0=2}\t{:0=11.4f}\t{:0=11.4f}\t{:0=11.4f}\t{:0=11.4f}\t{:0=11.10f}\t{:0=11.10f}".format(
lat, length_width, length_height, length_width / 60, length_height / 60, 1 / length_width, 1 / length_height))